折纸
前一段时间又发现了一件好玩的事:折纸。我小时候就挺喜欢折纸的,不过做的东西比较基础,例如纸船、千纸鹤、青蛙。这次在家里又开始学习了折纸,做了一些简单有趣的小玩意。
小时候折纸用的纸都很随意,直接拿 A4 纸了。这次我直接上网买了一套用来折纸的纸,主要是有各种颜色可以用来搭配,还有纸的厚度可能也更适合一些。有些作品,例如下面的刺猬,对纸的质量要求不低,我在做的时候明显可以看到有些折的比较多的地方已经破洞了。
我比较喜欢纯的折纸,不用胶水(因为没有)、剪刀。但是我能接受用手来裁(例如手动把一张正方形纸分成 4 份或者去掉一个角)。折完几个作品后,我觉得 modular origami 也很有趣,就是有点累……
盒子
这是我第一个作品,非常简单,几分钟就可以折好,我就当是练手了。前面几个作品我都是跟着 B 站上 up 主折纸的白叔 做的。这个作品的教程在这里(虽然 B 站的时候可以 embed 但是感觉没有必要)。为什么我会选择这个盒子来练手呢?因为这是当时白叔最新上传。


可以看到有些折痕没有对齐,还有很大的提升空间。但是 anyway,就是个热身。
钻石
这是第二个作品,同样是来自白叔,教程在这里。点击白叔主页,这是他 pin 住的代表作之一,那我就要来大力挑战一下了。

……感觉难度不大呀。这个作品就对纸张有一定的要求了,容易破。它比较有趣的一点在于下面自锁的结构。事实上,我折出来的自锁效果不好,但是看起来白叔的也不咋样,也是上了胶水,所以可能是设计问题。
玫瑰花
这个也是白叔 pin 起来的代表作,链接在此。准确的说,这个教程折的是川崎玫瑰。买家秀如下:
感觉这两个折的一般了……大红的那个是先折的,粉红的那个是第二次折的,把中间的芯弄大了一些。我后来查了一下,纸玫瑰除了川崎玫瑰之外,还有 PT 玫瑰和欧美玫瑰。于是我又去搞了一个 PT 玫瑰,依旧是白叔的教程,效果如下:
比之前的雍容富贵一些。欧美玫瑰我也看了,但是感觉对纸的要求很高就没搞了(其实更可能是因为懒)。PT 玫瑰的教程里,折了花芯之后,下一步需要把花瓣卷在一起,视频里说“整理”一下,这个“整理”我试了好久才找到一个勉强满意的整理方案,视频里也没说从哪个地方开始卷,哪个地方需要用手戳一戳抚平。最后展开花瓣的时候,我感觉我的纸已经快承受不住了,于是就随便搞了一下糊弄了事了……



五个相交四面体
这个是这几个作品我觉得最炫酷的一个,来自白叔的最高播放。先上效果图:

我当时做是参考的白叔的教程。我开始试图自己用对称性来搞,以为只要满足任意两个都相交就可以了,于是第三个四面体就瞎搞了一下,然后第四个四面体就傻眼了,找不到合适的位置了,于是又得反过去看视频。但是我觉得白叔也没有讲清楚这个结构的对称性以及如何利用对称性来找位置……
我们来仔细观察一下这个结构。它总共有 \(5 \times 4 = 20\) 个顶点,所以共有 10 对顶点,任意两种颜色之间有且仅有一对顶点。这个性质可以用来帮助我们定位还没有插进来的四面体的顶点了:假设我们一开始做好了红色和青色的四面体,现在要插一个紫色的进来。于是我们找一个还没有配对的红色顶点和一个还没有配对的青色顶点,并且它们距离合适,那么它们两个的对趾点就可以放一根紫色的边。我们还可以观察到:所有的边都刚好压住两条异色边,并且也刚好被两条异色边压住,而这条边在这个四面体上的对边则刚刚相反,这或许可以帮助我们在插边的时候确定上下位置。不过我也不知道只用这两条规则是否就足够了……
后来我闲逛的时候找到了这么一个网页(作者 Thomas Hull 之后会介绍),里面也提到
Unfortunately there's no easy way to describe how the tetrahedral frames need to weave around each other to create the 5 intersecting tetrahedra model.
不过这个网页里后面提供的几张图挺清楚的,感觉下次再折会很有帮助。这个网页还提到了一个很有趣的小问题:教程里用的都是 30 张 1x3 的长方形来做,每个长方形对应一条边。如果这个长方形太肥了,例如 1x2,边与边之间就会互相阻挡,后面的四面体就插不进去。那么这个长方形最肥的长宽比多少呢?
另外折之前可以好好思考调一下色,我这个颜色其实没选好……
刺猬
(不要吐槽绿色刺猬!都说了是奇行种!)

我看的 tutorial 是这个。但是在实际操作过程中,我觉得他折刺的过程可以改进:他的纸质量可能比较好,而且比较大,所以能够承受拉一下这个操作。我觉得一个更合理的方式是先把所有折痕折出来,然后再根据折痕折出刺的结构。稍微试一下就可以发现,折痕很好折,这样就避免了拉这个操作。还有一点需要注意的是:一开始找四分之一分界点的时候不要通过两次对折边来找,通过两次对折对角线来找会更好一些,因为接下来我们需要对一个 \(\frac{3}{4}\) 的正方形十六等分,这个要通过边对折来实现。如果两者都是通过边对折来实现,那么第二次的边对折被第一次边对折影响,找错了边就很尴尬(亲身经历)。
正方体环

我是在这里找到的一个正方体的教程,在这里看到的最后整体效果图。这个看起来没有五个相交四面体那么炫酷,但是看起来更和谐。更重要的是,这个作品耗费的体力远比五个相交四面体要大:五个相交四面体总共要折 \(5 \times 6 = 30\) 个相同的模块,但是这个作品需要 \(12 \times 12 = 144\) 个相同的模块,折完实在是累死了,但是也有很高的成就感。这个作品中有两种自锁结构:一个是这个环自己就是个锁,另外正方体的每个角也是一个自锁结构。正方体角的自锁结构比四面体的自锁结构要稳固一些。
这个结构中,所有的模块都是完全同构的,手性也是一样的。我一开始做的时候没注意,有一个模块的手性搞错了,就插不进去,最后不得不重折这个模块。
在组合两个小正方体的时候,我的方法是先折一个顶点,然后把这个顶点全部塞进之前做好的正方体内剩下的 9 条边就在正方体外组装。我看有的教程,例如这个,选择前一个正方体的最后一条边不组装,先把下一个正方体的顶点做好塞进去在组装,这也是可以的。最后一个正方体组装会非常麻烦,因为我得先把两个顶点组装好,各自塞进两个正方体,然后再在外面组装,这样的话可能首尾两个正方体各留一条边不组装,等最后一个用来连接的正方体差不多组装好了再组装最后一条边可能更好一些…… anyway 我是不想再试了,各位有兴趣的可以尝试一下新的方法。
一些小 trick
三等分一条边
在做五个相交四面体的时候,我们需要将一条边三等分。当时白叔用的方法很暴力,直接上尺子……有追求的同学想完全靠手,怎么办呢……我这里提供几种方法:
方法一:近似解(来源)。很简单,把这张纸用手卷成三份,然后鼓捣鼓捣,一边调整一边压实,然后就做出来了……说实话我不是很喜欢这种方法……
方法二:解析解(来源)。见下图:红圈是对角线的四等分点。
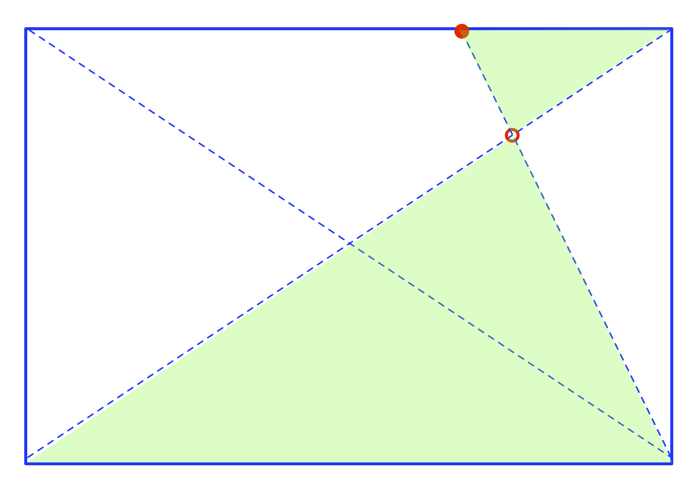
这在尺规作图中非常常见,我居然一开始居然没想到……
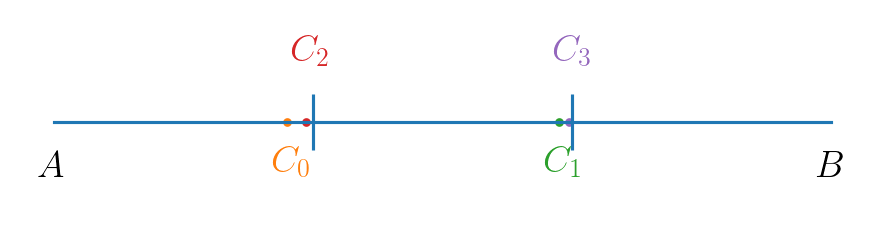
方法三:迭代解。不妨设我们想要三等分 \(AB\) 。于是我们先随便找一个初始解 \(C_0\),然后 \(C_1\) 为 \(C_0B\) 中点,\(C_2\) 为 \(AC_1\) 中点,\(C_3\) 为 \(C_2B\) 中点,\(C_4\) 为 \(AC_3\) 中点这样一路迭代下去。可以证明这个迭代是线性收敛的,所以初始的时候随便估一估,迭代几次就好了……
手动裁纸
在做五个相交四面体和正方体环的时候,我经常需要将一张纸裁成几份。由于我不喜欢用剪刀,所以我决定手裁。但是手裁的问题就是一不小心就容易分叉,另外一个问题是有毛边。毛边这个问题感觉不可避免,但是分叉这个问题还是可以解决的,trick 就是:假设你想沿着某条线裁下去,那就沿这条线折一下,不停用指甲按紧。注意要用指甲不能用指腹。按几次之后,把纸展开,还是沿之前那条线折一下,不过是反方向折(就是原来在外面的现在在里面了),继续用指甲按紧,感觉差不多了又翻过来继续按紧,这样重复几次,然后直接开始裁就行了。这个方法用了几百次,没有失手过。原理应该和金属疲劳差不多吧。
相关资料
五个相交四面体和正方体环都属于 modular origami,就是用一堆小模块来组装一个大结构。有一本书就叫做 Modular Origami Polyhedra ,Amazon 上给的封面就是正方体环。现在我已经整出正四面体和正六面体了,这里有正十二面体的教程。正二十面体的也有教程,正八面体可以不用 modular origami 做出来(教程,不过我还是喜欢 modular origami,但是没找到好看的),所以所有的正多面体都可以做出来了。
然后介绍一下 Thomas Hull,Western New England University 一个搞折纸的 Associate Professor。我之前引用的那个五个相交四面体的教程就是他的,我猜这个组装结构是他原创的(模块应该不是他发现的)。他发现了另外一个模块 PHiZZ,我在 Pinterest 上也看到了一些 PHiZZ 的创作,例如这个,确实很好看,就是 840 这个数字有点劝退……我光是正方体环 144 个模块就做的要死了……
说到搞折纸的教授,自然就不得不提一下 MIT 的 Erik Demaine,但是我没看他到底搞了啥,瞎猜是给定一个图形,如何科学地设计折痕,使得按照这个折痕能折出这个图形?他还是 Mihai Pătrașcu 的 PhD 导师,做 data structure 的人应该都知道 Mihai 这个名字。
(为什么又鸽了几个月?因为我之前把 Stephen's Sausage Roll 打通关了,但是感觉没啥可写的……)